

 |
 Hilfe zu "Pfiffikus" |
Um möglichst schnell zur Lösung zu kommen, empfiehlt es sich eine Taktik zu entwickeln, die eine möglichst zuverlässige Aussage über das Vorkommen bzw. Nichtvorkommen der verschiedenen Ziffern ermöglicht. Genauer: die zuverlässig über das Nichtvorkommen einzelner Ziffern Auskunft gibt.
Das kann zum Beispiel so aussehen:
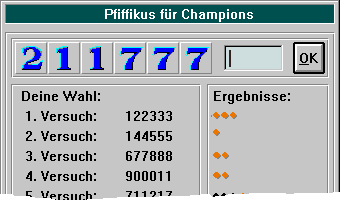
(Die Lösung ist in diesem Beispielbild bereits ermittelt, daher sind die blauen Fragezeichen bereits der Ergebnisanzeige gewichen.)
Was erkennen wir aus den verschiedenen Auswertungen der 9 Versuche ?
Ganz einfach:
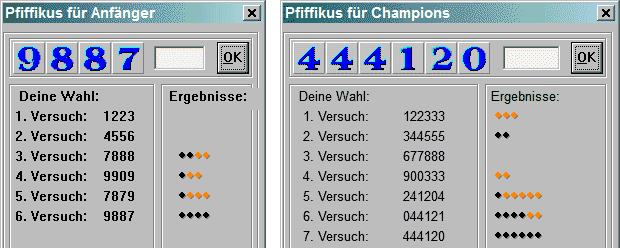
Versuch 1: Drei der eingetippten Ziffern sind richtig, also entweder kommt die 3 im Ergebnis vor oder die 1 und die 2.
Versuch 2: Also: es war die 1. 3, 4 und 5 scheiden somit aus, und auch die 2 ist richtig.
Versuch 3: Die 7 ist Bestandteil der gesuchten Zahl, aber 6 und 8 sind ganz sicher falsch.
Versuch 4: Die 9 und die 0 kommen ebenfalls nicht im Ergebnis vor.
Die einzigen Ziffern, die in der gedachten Zahl vorkommen, sind demzufolge:
1, 2 und 7.
Über die Anordnung, d.h. die Reihenfolge der Zahlen haben wir auch schon eine Menge herausbekommen, nämlich:
• Die 1 steht nicht an der ersten und nicht an einer der beiden letzten Stellen.
• Die 2 steht weder an der zweiten noch an der dritten Stelle.
• Die 7 steht weder an der zweiten noch an der dritten Stelle.
Jetzt müssen wir probieren, und unser Vorschlag muss den bisher gewonnenen Erkenntnissen entsprechen:
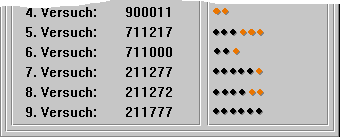
Versuch 5: Schon ganz ordentlich. ... Gemerkt ? Kleiner Tippfehler ? Die 1 an der vorletzten Stelle ... das war nicht so gut.
Aber egal, gleich noch was zum Kontrast: Jetzt benutzen wir absichtlich eine falsche Zahl, um die Reihenfolge genauer bewerten zu können, und:
Versuch 6: Immerhin, in den ersten drei Ziffern zwei Treffer. Aber das will noch nichts heißen ...
Versuch 7: Oha, das war Glückssache ... Aber eine der Ziffern entspricht nicht den Erwartungen unseres elektronischen Schiedsrichters. Da wir alle denkbaren Ziffern verwendet haben, ist also eine der Mehrfachnennungen auszutauschen.
Das probieren wir aus, und zwar im
Versuch 8 und Versuch 9, wobei wir auf die in den ersten vier Versuchen ermittelten Ausschlüsse achten. Und siehe da, es war gar nicht so schwer !
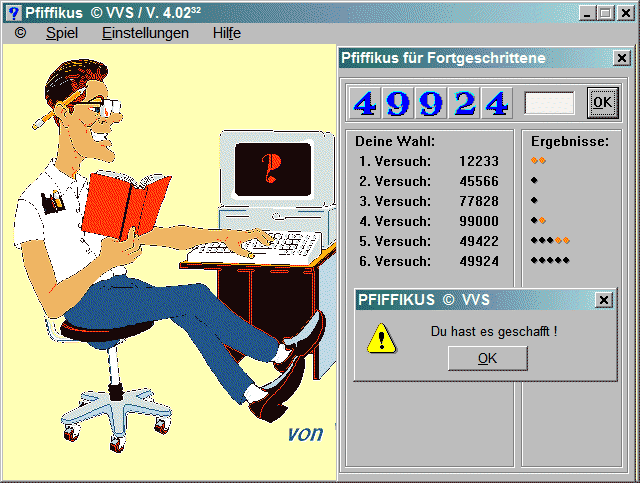
Wir probieren es noch einmal mit der fünfstelligen Version.
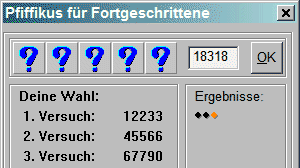
Wie es der Zufall will ... aus den ersten drei Vorschlägen sehen wir, dass die Ziffern 4, 5, 6, 7, 9 und 0 überhaupt nicht im Ergebnis vorkommen. Wir wissen aber, dass die 1 ganz sicher richtig ist und dass entweder die 2 oder die 3 ebenfalls dabei ist. Das macht das weitere Vorgehen zunächst mal leicht, denn die einzige Ziffer, die wir noch nicht geprüft haben, ist die 8.
Wir versuchen mal, sie einzubauen (4. Versuch) und gehen zunächst einfach davon aus, dass die 1 die erste Stelle innehat.
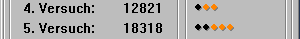
Das hat ja gut geklappt. Denn: drei Ergebnispunkte sagen uns: die 8 ist ganz sicher dabei ... und eine der anderen beiden Ziffen. Da wir die 1 schon als sicheren Kandidaten ermittelt haben, kann es die 2 nicht sein. Daraus folgt zwingend, dass die 3 im Ergebnis vorkommen muss. Damit ist es sicher: Nur 1, 3 und 8 bilden die vom Computer ausgedachte Zahl.
Nun müssen wir es ausprobieren ... 5. Versuch ... noch nicht so ganz, also gleich noch einer ...
Das ist doch schon nah dran.

Der Rest besteht dann im Grunde nur noch im Ausprobieren der möglichen Doppelungen.
Und das war's dann auch schon. Hätte auch schon eher klappen können.
Und noch etwas zur Eigenanalyse:
Manchmal läuft's einfach ... sechs bis neun Versuche kann man als gutes Ergebnis werten.