

 |
 Hilfe zu "Pfiffikus" |
Eigentlich kann man Pfiffikus recht schnell intuitiv begreifen. Ich will aber doch rasch ein paar Worte zum Spielverlauf und insbesondere zur Auswertung der eingetippten Lösungsvorschläge verlieren.
Ziel des Spiels ist es, eine vom Computer ausgedachte Zufallszahl zu erraten. Wie das im Spielverlauf funktioniert, erkennt man sicher auch ohne viele Hilfen. Aber es gibt einige Kleinigkeiten zu beachten:
Die Zahl der Stellen, die die gedachte Zahl aufweist, ist an der Zahl der blauen Fragezeichen zu erkennen. Um die Zahl herauszutüfteln, musst du eine Zahl entsprechender Länge in das Eingabefeld eintragen und anschließend den OK-Knopf anklicken oder die RETURN-Taste drücken.
Was passiert jetzt ? Aufgepasst:
Der Computer vergleicht jetzt deine eingetippte Zahl Ziffer für Ziffer (!) mit seiner "gedachten" Zahl und zeigt das Ergebnis seiner Überlegungen in folgender Form an:
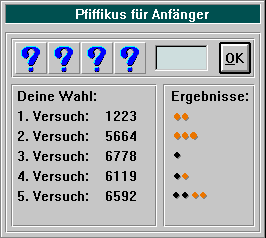
Die Bewertung deines eingetippten Lösungsvorschlages wird durch orangefarbene und schwarze Merker sichtbar gemacht.
Dabei bekommst du folgende Ergebnispunkte:
• einen orangefarbenen Merker für jede in deinem Vorschlag enthaltene Ziffer, die in der gedachten Zahl vorkommt, aber
• stattdessen (!) einen schwarzen Merker, wenn ebendiese Ziffer in der gedachten Zahl an derselben Stelle steht wie in deinem Vorschlag.
Die Ausgabe erfolgt immer in der Reihenfolge "erst schwarz, dann orangefarben", sie gibt also keinen unmittelbaren Aufschluss darüber, welche der eingegebenen Ziffern richtig platziert ist.
Also bedeutet dies in dem oben dargestellten Beispiel genau Folgendes:
1. Versuch: Zwei der eingetippten Ziffern finden sich in der gedachten Zahl wieder. Das können entweder die 1 und die 3 sein, oder es handelt sich um die 2. (Keine von ihnen ist richtig plaziert.)
Wäre es die 2, so bedeutete dies aber nicht, dass die gedachte Zahl diese gefundene Ziffer mehrfach enthielte !
2. Versuch: Drei der eingetippten Ziffern haben eine Entsprechnung in der gedachten Zahl und wieder ist keine von ihnen richtig plaziert. Es handelt sich aber ganz sicher um die 6 und eine weitere Ziffer, also entweder die 4 oder die 5.
3. Versuch: Nur eine der eingegebenen Ziffern ist im Ergebnis enthalten, und diese steht auch an derselben Stelle. Im Zusammenhang mit den ersten beiden Versuchen ist klar, dass es sich dabei um die 6 handeln muss.
4. Versuch: Eine weitere eingetippte Ziffer ist in der gedachten Zahl enthalten, logisch, dass dies nur die 9 sein kann, denn bei der 1 hätte es ja zwei weitere Ergebnispunkte (egal ob orangefarben oder schwarz) geben müssen. Nun wird's langsam klar, wie es weitergehen muss:
Dass die 1 nicht richtig ist, erkennen wir rückschauend aus dem ersten Versuch, da auch die 3 nicht stimmt, die 2 ist also ganz sicher unser Kandidat. Und sie kann nur an der letzten Stelle stehen, weil vorn die 6 ist und im ersten Versuch keine der eingegebenen Ziffern richtig plaziert war.
Also schon sicher: 6 - - 2.
Außerdem wissen wir aus dem 2. Versuch, dass 4 oder 5 richtig sein muss. Die verbleibenden Lösungsmöglichkeiten sind also 6492, 6592 6942 und 6952. Da hilft nur: ausprobieren !
5. Versuch: Und schon ist alles klar. Sämtliche vier Ziffern sind richtig erraten, nur zwei sind falsch plaziert. Da die erste und letzte Stelle bereits feststehen, können nur die beiden mittleren miteinander vertauscht werden.
Und siehe da: Der Comupter denkt auch so:
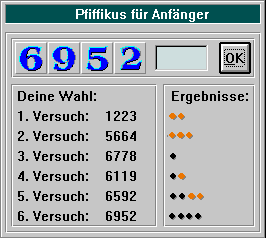
In der fünfstelligen Version von Pfiffikus kann man 12 Versuche machen, bevor der Computer die Runde abbricht. Im allgemeinen schafft man es aber mit sechs bis acht, höchstens mal zehn Versuchen. In der vierstelligen Variante sind es 10, in der sechsstelligen 15 mögliche Versuche.
Die "gedachte Zahl" wird natürlich über einen ziemlich guten Zufallsgenerator erzeugt, es gibt daher keine Beschränkungen in der Anzahl der mehrfach auftretenden Ziffern. Alle Zahlen von "0000" bis "9999" (bzw. "00000" bis "99999" oder "000000" bis "999999") sind möglich !
(Vorlaufende Nullen müssen im Lösungsvorschlag immer eingegeben werden !)